Laiko ribojimas: 1s

Atminties ribojimas: 64MB

Jei norite pateikti savo sprendimą - prisijunkite.

Grafo spalvinimas

Barbora visai neseniai pradėjo mokytis grafų teorijos pradmenų. Mergaitė kiek pavargo dėl didelio naujos informacijos kiekio, tad nusprendė padaryti pertrauką. Barbora labai mėgsta spalvinti, todėl ji pasiėmė savo mėgstamą spalvinimo knygelę, atsivertė naują puslapį ir ten pamatė... grafą!

"Ech, juk norėjau nuo grafų pailsėti. Ir šiaip, čia nelabai yra ką spalvinti - neįdomu. Nebent..."

Mergaitė pradėjo galvoti, kaip būtų galima grafą nuspalvinti kuo įdomiau. Ji nusprendė, kad spalvins tik grafo viršūnes, bet ne bet kaip - ji nori, kad gretimos viršūnės visada būtų nuspalvintos skirtingomis spalvomis.

Vis dėlto, ši užduotis Barborai taip pat per lengva - juk tiesiog galima visas viršūnes nuspalvinti skirtingomis spalvomis ir tai tenkins mergaitės sugalvotą salygą... Todėl Barbora nusprendė atrasti, kiek mažiausiai spalvų reikia, kad pavyktų nuspalvinti visas grafo viršūnes pagal sugalvotą taisyklę.

Panagrinėkime pavyzdį. Tarkime, kad Barbora savo knygutėje rado tokį grafą:

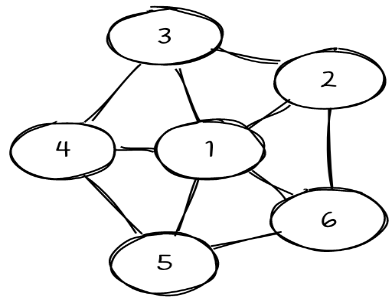
Grafas

Vienas iš galimų būdų nuspalvinti grafo viršūnes yra visas jas spalvinti skirtingomis spalvomis - tuomet prireiks šešių spalvų:

Grafas su šešiomis spalvomis

Kai kurias viršūnes galima spalvinti ta pačia spalva, nes jos neturi bendros briaunos. Tada jau užtektų ir penkių spalvų:

Grafas su penkiomis spalvomis

Galima pasiekti ir dar geresni rezultatą panaudojus keturias spalvas:

Grafas su keturiomis spalvomis

Mažiau spalvų panaudoti neįmanoma. Žemiau pateiktas pavyzdys su trimis spalvomis, tačiau jis nėra tinkamas, nes viršūnes 5 ir 6 jungia briauna, bet jos abi nuspalvintos ta pačia spalva:

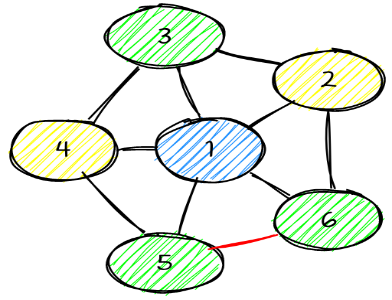
Blogai nuspalvintas grafas

Ši užduotis Barborai jau pasirodė kiek per sunki, todėl ji paprašė Jūsų pagalbos. Parašykite programą, kuri rastų, kiek mažiausiai spalvų reikia, kad būtų galima nuspalvinti visas grafo viršūnes taip, kad visos gretimos viršūnės būtų nuspalvintos skirtingomis spalvomis.

Pradiniai duomenys

Pirmoje eilutėje pateikti du sveikieji skaičiai n ir m - grafo viršūnių ir briaunų kiekiai (1\\leqn\\leq8,0\\leqm\\leq\\frac{n(n-1)}{2}).

Toliau pateikta m eilučių. i-ojoje iš jų yra du tarpu atskirti sveikieji skaičiai u_i ir v_i, reiškiantys, kad tarp viršūnių u_i ir v_i yra briauna. Yra garantuota, kad nebus pasikartojančių briaunų bei kilpų.

Rezultatai

Jūsų programa turi išvesti vieną sveikąjį skaičių - kiek mažiausiai spalvų prireiks, kad pavyktų nuspalvinti visas grafo viršūnes pagal aprašytas taisykles.

Pavyzdžiai

Pradiniai duomenys Rezultatai Paaiškinimas 
6 10
1 2
1 3
1 4
1 5
1 6
2 3
3 4
4 5
5 6
6 2
 
4
 Pavyzdys atitinka sąlygoje aptartą grafą 
3 1
1 2
 
2
 Pavyzdys 
4 0
 
1
 Pavyzdys