Šeštadieninė informatikos olimpiadininkų mokykla

Hanojaus bokštų uždavinį 1883 metais suformulavo prancūzų matematikas Eduardas Lukas (Edouard Lucas). Duoti trys stiebai ir aštuoni skirtingo dydžio diskai. Iš pradžių visi šie diskai sumauti ant pirmojo stiebo: apačioje pats didžiausias diskas, ant jo – mažesnis ir t. t. Viršuje užmautas pats mažiausias iš diskų. Uždavinys prašo perkelti visus diskus nuo pirmojo stiebo ant paskutiniojo laikantis tokių taisyklių:

• Vienu ėjimu galima kelti tik vieną diską.
• Diską galima užmauti tik ant tuščio stiebo, arba uždėti ant didesnio už jį disko.

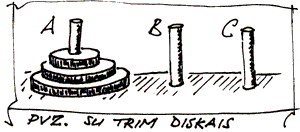
Mes praplėsime standartinę uždavinio formuluotę: vietoje aštuonių, reikia perkelti N diskų. Mūsų uždavinyje stiebai yra pavadinti raidėmis A, B ir C. Parašykite programą, kuri atspausdintų ėjimus, kuriuos reikia atlikti, kad diskus perkeltume nuo stiebo A ant stiebo C, laikantis minėtųjų taisyklių. Atliekamų ėjimų skaičius turi būti minimalus.

Pradiniai duomenys

Pradinių duomenų faile įrašytas vienintelis sveikas skaičius N () – diskų skaičius.

Rezultatai

Rezultatų failą turi sudaryti seka ėjimų, kuriuos atlikus, visi diskai būtų perkelti nuo stiebo A ant stiebo C. Ėjimas aprašomas formatu X -> Y (čia X ir Y yra stiebų vardai A, B arba C). Užrašas X -> Y reiškia, kad nuo stiebo X reikia paimti mažiausią (taigi viršuje esantį) diską ir užmauti ant stiebo Y.

Pavyzdžiai

3

A -> C
A -> B
C -> B
A -> C
B -> A
B -> C
A -> C