ŠIOM — Karosai (LMIO 2018/2019)

Laiko ribojimas: 1s

Atminties ribojimas: 64MB

Language:
Source file:
Jei norite pateikti savo sprendimą - prisijunkite.

Karosai (LMIO 2018/2019)

Karosas Rosas plaukioja tvenkinių sistemoje, sudarytoje iš $N$ tvenkinių. Kai kurių iš tvenkinių yra sujungti, taigi galima perplaukti iš vieno į kitą. Tačiau juos skiria tam tikro aukščio pertvara, kurią žymėsime $h_{i,j}$ (be abejo, $h_{i,j}=h_{j,i}$ ). Karosai gali perplaukti iš tvenkinio $i$ į tvenkinį $j$ tik tuomet, kai vandens lygis tvenkinyje $i$ yra nemažesnis nei $h_{i,j}$ .

Pavyzdžiui, yra trys tvenkiniai ( $N=3$ ), pirmas ir antras tvenkiniai yra sujungti pertvara, kurios aukštis $h_{1,2}=5000$ , o antras ir trečias - pertvara, kurios aukštis $h_{2,3}=7000$ . Karosai galės perplaukti iš pirmo tvenkinio į antrą, jeigu vandens lygis pirmame (taigi ir antrame) tvenkinyje sieks bent $5000$ . Tačiau, jie galėtų perplaukti iš pirmo į trečią tvenkinį, tik jei vandens lygis sieks $7000$ .

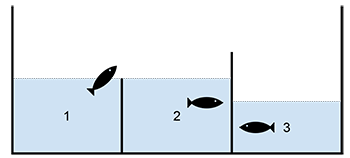
Pavyzdys

Karosas Rosas yra apsistojęs 1-ame tvenkinyje, o jo draugas - tvenkinyje nr. $N$ . Rosui rūpi, koks turi būti vandens lygis 1-ame tvenkinyje, kad jis galėtų aplankyti savo draugą.

Užduotis

Duota tvenkinių konfigūracija. Raskite, kiek mažiausiai turi būti pakeltas vandens lygis 1-ame tvenkinyje, kad iš jo būtų įmanoma pasiekti $N$ -ąjį tvenkinį.

Pradiniai duomenys

Pirmoje eilutėje įrašyti du sveikieji skaičiai: tvenkinių skaičius $N$ bei sujungtų tvenkinių porų skaičius $M$ .

Toliau pateikta $M$ eilučių, kuriose aprašytos sujungtų tvenkinių poros. Kiekvienoje iš eilučių pateikta po tris sveikuosius skaičius: $i$ , $j$ , $h_{i,j}$ , kurie žymi, kad tvenkiniai $i$ ir $j$ yra sujungti pertvara, kurios aukštis $h_{i,j}$ . ( $1\\leqi\\lej\\leqN$ , taip pat laikykite, jog $h_{i,j}=h_{j,i}$ ).

Rezultatai

Išveskite vienintelį sveikąjį skaičių - minimalų vandens lygį pirmajame tvenkinyje, kuris būtinas, kad iš jo būtų galima pasiekti $N$ -ąjį tvenkinį.

Duomenys tokie, kad visuomet yra galimas kelias iš tvenkinio $1$ į tvenkinį $N$ .

Pavyzdžiai

Pradiniai duomenys	Rezultatai	Paaiškinimas
3 2 1 2 5000 2 3 7000	7000	Sąlygoje nagrinėtas pavyzdys
4 5 1 2 5000 1 3 2000 1 4 10000 2 4 4000 3 4 3000	3000	Jei pirmame kanale aukštis bus pakeltas iki $3000$ , tai Rosas galės perplaukti į 3-iąjį kanalą, o iš ten - į 4-ąjį.

Ribojimai

$1\\leN\\le1000;$

$0\\leM\\le\\frac{N(N-1)}{2};$