Laiko ribojimas: 1s

Atminties ribojimas: 64MB

Jei norite pateikti savo sprendimą - prisijunkite.

Medkirtys

Medkirtys Mantas laisvalaikiu mėgsta kapoti medžius. Tik, žinoma, ne tuos, kurie auga lauke, o tuos, kuriuos nagrinėja grafų teorija (juk gamtos niokoti negalima). Šiandien Mantas sugalvojo naują medžių kapojimo būdą. Kadangi vaikinui labai patinka lyginiai skaičiai, jis nori medį sukapoti taip, kad kiekvienoje atkirstoje dalyje liktų lyginis skaičius viršūnių. Šį kapojimo būdą Mantas nusprendė išbandyti su neseniai rastu medžiu, tačiau uždavinys pasirodė ne toks paprastas, tad jam prireikė jūsų pagalbos.

Formaliai tariant, jums duotas medis (jungus grafas be ciklų), turintis N viršūnių. Be to, N yra lyginis skaičius. Jūsų užduotis yra surasti, kiek daugiausiai briaunų galima pašalinti iš šio medžio taip, kad kiekvienoje iš likusių jungiųjų komponenčių liktų lyginis skaičius viršūnių.

Pradiniai duomenys

Pirmoje eilutėje pateiktas vienas sveikasis skaičius N - medžio viršūnių kiekis (1\\leqN\\leq2\\cdotp10^5).

Toliau seka N-1 eilučių. i-ojoje iš jų yra pateikti du sveikieji skaičiai u ir v, reiškiantys, kad viršūnes u ir v jungia briauna (1\\lequ,v\\leqN).

Rezultatai

Jūsų programa turi išvesti vieną sveikąjį skaičių - kiek daugiausiai briaunų galima pašalinti iš medžio, kad būtų tenkinamos uždavinio sąlygos.

Pavyzdžiai

Pradiniai duomenys Rezultatai Paaiškinimas 
10
2 1
3 1
4 3
5 2
6 1
7 2
8 6
9 8
10 8
 
2
 Briaunos, kurias galima pašalinti, pažymėtos punktyrine linija: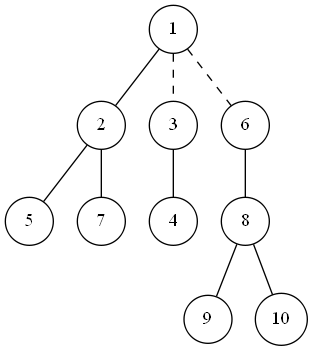
pavyzdys