Laiko ribojimas: 1s

Atminties ribojimas: 64MB

Duomenų failas: mountain.in

Rezultatų failas: mountain.out

Jei norite pateikti savo sprendimą - prisijunkite.

Kalnai

Kalnų atrakcionų parkas atidarė naują amerikietiškų kalnelių atrakcioną, kurį sudaro geležinkelis iš n bėgių atkarpų, sujungtų viena su kita galais. Pirmosios atkarpos pradžios taškas yra nuliniame (0) aukštyje. Atrakciono prižiūrėtojas Baitmanas gali perkonfigūruoti geležinkelį pakeisdamas keleto nuosekliai sujungtų bėgių atkarpų aukščių pokyčius (aukščio pokytis – atkarpos galo ir pradžios aukščių skirtumas). Likusių bėgių atkarpų aukščių pokyčiai lieka tie patys. Kiekvieną kartą, kai perkonfigūruojamas atrakcionas, toliau esanti geležinkelio dalis pakeliama arba nuleidžiama, nes būtina, kad visas geležinkelis liktų sujungtas, o pradžios taškas pasiliktų nuliniame aukštyje.

Kiekvienas važiavimas pradedamas įkraunant traukinuko akumuliatorių tiek, kad traukinukas galėtų pasiekti aukštį h. T.y. traukinukas važiuos tol, kol geležinkelio pakilimo aukštis neviršys h arba kol bus pasiektas geležinkelio galas (jei traukinukas negali pasiekti bėgio atkarpos galo, tai ta atkarpa jis visai nevažiuoja).

Žinomi duomenys apie visus vienos dienos važiavimus (važiavimą nusako aukštis h) ir visus konfigūracijos pakeitimus. Kiekvienam važiavimui reikia apskaičiuoti, kiek bėgių atkarpų pervažiavo traukinukas iki sustodamas.

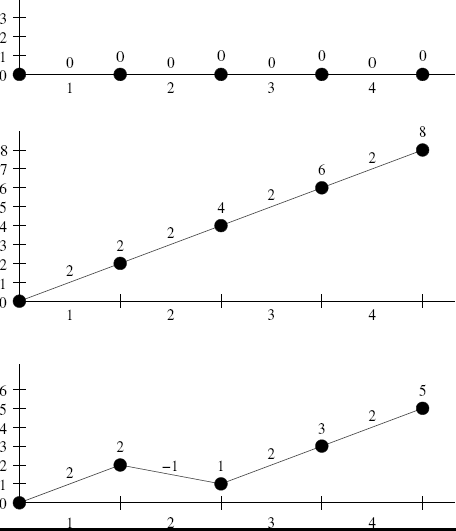
Atrakciono konfigūraciją nusako visų n bėgių atkarpų aukščių pokyčių seka (vienas pokytis apibūdina vieną atkarpą). i-asis šios sekos skaičius d_i nusako i-osios atkarpos galo ir pradžios aukščių pokytį centimetrais.

Pavyzdžiui, traukinukas pravažiavo i-1 bėgių atkarpų ir pasiekė hh centimetrų aukštį. Tai reiškia, kad pravažiavęs i bėgių atkarpų, traukinukas bus pasiekęs hh+d_i centimetrų aukštį.

Pradiniu momentu visos bėgių atkarpos yra horizontalioje padėtyje, t.y. kiekvienam i d_i=0. Važiavimai ir perkonfigūravimai gali vykti įvairia tvarka. Kiekvieną perkonfigūravimą nusako trys skaičiai: a, b ir D. Tai reiškia, kad perkonfigūruojamos bėgių atkarpos nuo a iki b (imtinai). T.y. visų šio segmentų atkarpų aukščių pokyčiai taps lygūs D: d_i=D visiems a\\lei\\leb.

Kiekvieną važiavimą nusako vienas skaičius h – maksimalus aukštis, kurį gali pasiekti traukinukas.

Parašykite programą, kuri kiekvienam važiavimui apskaičiuotų, kiek bėgių atkarpų kirto traukinukas.

Pradiniai duomenys

Pirmoje eilutėje pateiktas vienas teigiamas skaičius n. Tai bėgių atkarpų skaičius, 1\\len\\le10^9.

Tolesnėse eilutėse įrašyti geležinkelio perkonfigūravimai besikeičiantys su važiavimais. Šią eilučių seką užbaigia eilutė su pabaigos ženklu. Kiekviena eilutė yra vieno iš trijų pavidalų:

  • Perkofigūravimas – raidė I ir sveikieji skaičiai a, b ir D, atskirti vienu tarpu (1\\lea\\leb\\len, -10^9\\leD\\le10^9).
  • Važiavimas – raidė Q ir sveikasis skaičius h, (0\\leh\\le10^9), atskirti vienu tarpu.
  • Pabaigos ženklas – raidė E, kuri rodo duomenų rinkinio pabaigą.

Laikykite, kad bet kuriuo momentu pakilimas bet kuriame geležinkelio taške yra iš intervalo [0,10^9] matuojant centimetrais. Pradinius duomenis sudaro ne daugiau kaip 10^5 eilučių.

Rezultatai

Pateikiamų rezultatų i-toje eilutėje turi būti įrašytas vienas sveikasis skaičius – bėgių atkarpų, kurias pervažiavo traukinukas, i-ojo važiavimo metu.

Pavyzdys

Duomenys Rezultatai 
4
Q 1
I 1 4 2
Q 3
Q 1
I 2 2 -1
Q 3
E
 
4
1
0
3

Pavyzdys