Laiko ribojimas: 1s

Atminties ribojimas: 64MB

Duomenų failas: points.in

Rezultatų failas: points.out

Jei norite pateikti savo sprendimą - prisijunkite.

Taškų jungimas

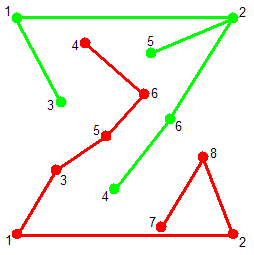
Pavyzdys

Žaidžia vienas žaidėjas. Pasirenka du didesnius už 2 sveikuosius skaičius, tarkime, g ir r. Tada padeda keturis taškus taip, kad jie sudarytų kvadrato kampus: viršuje – du žalius, apačioje – du raudonus. Toliau kvadrato viduje žymi žalius ir raudonus taškus taip, kad jokie trys taškai, įskaitant ir keturis pradinius, nebūtų vienoje tiesėje. Šitaip daroma tol, kol bendras žalių taškų skaičius tampa lygus g, o raudonų – r.

Kai taškai sudėlioti, pradedama jungti. Bet kurie du taškai gali būti sujungti atkarpa, jei:

  • jie yra tos pačios spalvos ir
  • brėžiama atkarpa nekerta jokios anksčiau nubrėžtos atkarpos (išskyrus taškus atkarpų galuose).

Sakoma, kad du taškai u ir v yra tame pačiame komponente, jei iš taško u galima patekti į tašką v einant tik jau nubrėžtomis atkarpomis.

Žaidimas laimimas, jei visi žali taškai yra viename komponente, sudarytame iš lygiai g-1 atkarpų, o visi raudoni taškai – kitame komponente, sudarytame iš r-1 atkarpų.

Duota pradinė situacija, t.y. kvadratiniame s\\timess dydžio lape sužymėta g žalių ir r raudonų taškų, kiekvieno kurių koordinatės (x_i, y_i) yra sveikieji skaičiai. Žali taškai sunumeruoti nuo 1 iki g: viršutiniame kairiajame kampe yra taškas, kurio numeris 1, jo koordinatės – (0, s), viršutiniame dešiniajame – taškas, kurio numeris 2, jo koordinatės – (s, s), o vidiniai taškai numeruojami nuo 3 iki g. Raudoni taškai numeruojami nuo 1 iki r: apatiniame kairiajame kampe yra taškas, kurio numeris 1 ir koordinatės (0, 0), apatiniame dešiniajame – taškas, kurio numeris 2 ir koordinatės (s, 0), o vidiniai taškai numeruojami nuo 3 iki r.

Parašykite programą, kuri nustatytų, kaip nubrėžti g-1 žalią ir r-1 raudonas atkarpas taip, kad visos žalios atkarpos būtų viename komponente, o visos raudonos – kitame ir jokios dvi atkarpos nesikirstų.

Pradiniai duomenys

Pirmoje eilutėje yra vienas sveikasis skaičius g (3\\leg\\le50~000). Tolesnėse g eilutėse yra po du tarpu atskirtus sveikuosius skaičius – žalių taškų koordinatės x_i ir y_i. Taškai pateikiami nuo jų numerių didėjimo tvarka.

Tolesnėje eilutėje yra vienas sveikasis skaičius r (3\\ler\\le50~000). Tolesnėse r eilutėse yra po du tarpu atskirtus sveikuosius skaičius – raudonų taškų koordinatės x_i ir y_i. Taškai pateikiami nuo jų numerių didėjimo tvarka.

Visi taškai yra s\\timess kvadrato ribose (0<s\\le200~000~000)

Rezultatai

Rezultatus turi sudaryti (g-1)+(r-1) eilučių – kiekvienai nubrėžtai atkarpai skiriant po vieną eilutę. Kiekvieną atkarpą apibūdina trys tarpais atskirti duomenys: du sveikieji skaičiai ir raidė atkarpos spalvai nusakyti. Sveikieji skaičiai yra taškų, sujungtų šia atkarpa, numeriai. Jei sujungti taškai yra žali, rašoma g raidė, jei raudoni – r raidė. Nei atkarpų, nei kiekvienos atkarpos galinių taškų pateikimo tvarka nėra svarbi.

Pavyzdys

Duomenys Rezultatai 
6
0 1000
1000 1000
203 601
449 212
620 837
708 537
8
0 0
1000 0
185 300
314 888
416 458
614 622
683 95
838 400
 
1 3 g
3 1 r
3 5 r
4 6 r
6 5 r
4 6 g
1 2 g
1 2 r
5 2 g
2 6 g
7 8 r
8 2 r