Laiko ribojimas: 1s

Atminties ribojimas: 64MB

Jei norite pateikti savo sprendimą - prisijunkite.

Senamiestis

Gabrielius nusipirko naują dviratį ir nusprendė jį išmėginti. Akivaizdu, kad geriausias būdas išbandyti dviratį yra su juo pasivažinėti. Pasivažinėjimui Gabrielius išsirinko Vilniaus senamiesčio gatves. Kaip turbūt žinote, senamiestyje galima rasti labai daug vienpusio eismo gatvių, t.y. tokių gatvių, kuriomis galima važiuoti tik viena kryptimi. Šiandien viskas yra dar įdomiau - įsigaliojo naujas įstatymas, kuris visas gatves padarė vienpusio eismo. Taip pat, buvo užtikrinta, kad gatvės nesudarys ciklų (t.y. iškeliavus iš tam tikro miesto, į jį grįžti tampa nebeįmanoma).

Formaliai, Vilniaus senamiestį sudaro N sankryžų, kurios tarpusavyje sujungtos M vienpusių kelių. Kiekvieną kelią apibūdina trys skaičiai (u,v,w), reiškiantys, kad keliu galima važiuoti iš sankryžos u į sankryžą v (bet ne atvirkščiai), o to kelio ilgis yra w. Sankryžos yra sunumeruotos nuo 1 iki N.

Vienoje savaitgalinėje tam tikro dalyko mokykloje Gabrielius jau mokėsi apie trumpiausio kelio paieškas, tačiau norint išbandyti dviratį juk reikėtų pavažinėti kuo ilgiau! Taigi, Gabrielius, žinodamas Vilniaus senamiesčio gatvių išplanavimą bei sankryžą, nuo kurios pradės kelionę, nori surasti patį ilgiausią kelią, prasidedantį jo sankryžoje ir besibaigiantį kažkurioje kitoje sankryžoje. Deja, šis uždavinys pasirodė ne toks paprastas, kaip buvo galima pamanyti. Pabandykite jį išspręsti ir jūs!

Pradiniai duomenys

Pirmoje eilutėje pateikti trys sveikieji skaičiai N, M ir s - atitinkamai sankryžų ir kelių kiekiai bei sankryža, kurioje bus pradėta kelion (1\\leqN\\leq10^5,0\\leqM\\leq2\\cdotp10^5,1\\leqs\\leqN).

Toliau seka M eilučių. i-ojoje iš jų pateikti trys skaičiai u, v ir w, apibūdinantys i-ąjį kelią (1\\lequ,v,\\leqN,1\\leqw\\leq10^9). Galite tarti, kad nėra kelių, prasidedančių ir pasibaigiančių toje pačioje sankryžoje. Taip pat, keliai tikrai nesudarys ciklų.

Rezultatai

Jūsų programa turi išvesti vieną sveikąjį skaičių - ilgiausią įmanomą kelią, jei kelionė pradedama sankryžoje s.

Pavyzdžiai

Pradiniai duomenys Rezultatai 
3 3 1
1 2 1
2 3 1
1 3 1
 
2
 
3 3 2
1 2 1
2 3 1
1 3 1
 
1
 
3 3 3
1 2 1
2 3 1
1 3 1
 
0
 
9 10 2
1 2 100
2 3 1
2 4 2
3 5 1
4 5 8
5 6 5
6 7 1
6 8 5
7 9 14
8 9 5
 
30

Paaiškinimai

Pirmieji trys pavyzdžiai aprašo tokį sankryžų ir kelių išsidėstymą:

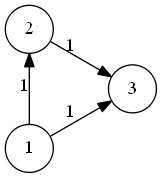
pavyzdys123

Pirmajame teste Gabrielius pradės sankryžoje 1, tad ilgiausio kelio, prasidedančio čia, ilgis yra 2 (pats kelias yra 1 -> 2 -> 3).

Antrajame teste Gabrielius pradeda 2 sankryžoje, tad iš ten tėra vienas galimas kelias, kurio ilgis 1.

Trečiajame teste Gabrielius pradeda 3 sankryžoje, iš kurios neišeina nė vienas kelias, tad dviračio išbandyti nepavyks.

Ketvirtasis testas atrodo taip (pilkai paryškinta pradinė sankryža, o mėlynai - ilgiausias kelias):

pavyzdys4